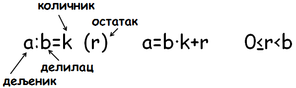Дељивост у No, основна својства
Пример: Мајка је купила 12 балона за своје 4 ћерке. Да ли може поделити балоне тако да свака од ћерки добије једнак број балона? Шта би се десило да је купила 15 балона?
На примеру сазнајемо да резултат дељења два природна броја не мора да буде природан број. Упоредити то са одузимањем, за разлику од сабирања и множења природних бројева када је резултат природан број.
Деф: Ако је а:b природан број, тада кажемо да број b дели број а или а је дељиво са b, што записујемо са b∣a. Ако је а:b природан број, то значи да постоји неки број природан број k, такав да је а=b∙k. Ако број b не дели број а, то записујемо тако што цртицу прецртамо.
Дакле, један природан број није увек могуће поделити другим, али дељење са остатком је увек могуће.
Деф: Дељење са остатком броја а бројем b јесте одређивање бројева k и r, таквих да је а=bk+r , где је а дељеник, b делилац, k количник и r остатак.
Остатак при дељењу броја а бројем b је већи или једнак нули, а мањи од делиоца b. Ако је остатак при дељењу броја а бројем b једанак нули, тада је а дељиво са b.
На примеру сазнајемо да резултат дељења два природна броја не мора да буде природан број. Упоредити то са одузимањем, за разлику од сабирања и множења природних бројева када је резултат природан број.
Деф: Ако је а:b природан број, тада кажемо да број b дели број а или а је дељиво са b, што записујемо са b∣a. Ако је а:b природан број, то значи да постоји неки број природан број k, такав да је а=b∙k. Ако број b не дели број а, то записујемо тако што цртицу прецртамо.
Дакле, један природан број није увек могуће поделити другим, али дељење са остатком је увек могуће.
Деф: Дељење са остатком броја а бројем b јесте одређивање бројева k и r, таквих да је а=bk+r , где је а дељеник, b делилац, k количник и r остатак.
Остатак при дељењу броја а бројем b је већи или једнак нули, а мањи од делиоца b. Ако је остатак при дељењу броја а бројем b једанак нули, тада је а дељиво са b.
Својства дељивости
* Сваки природан број дељив је јединицом и самим собом.
Пример: Ана има 36 бомбона, а Ивана 48 бомбона. Да ли свака од њих може поделити своје бомбоне у кесице тако да у свакој кесици буду по 4 бомбоне? Ако обједине своје бомбоне да ли их тада могу сместити у кесице по 4 бомбоне?
Дакле, ако 4∣36 и 4∣48, тада и 4∣(36+48). Ово је лако показати, јер ако је 36=4·9 и 48=4·12, тада је 36+48=4·9+4·12=4·(9+12), односно 4∣(36+48). Међутим, ако сабирци нису дељиви неким бројем то не значи да и збир није дељив тим бројем.
Нпр. 2 не дели 17 и 2 не дели 15, али 2 дели 17+15. Исто важи иза разлику.
* Ако су сабирци дељиви неким бројем, онда је и збир дељив тим бројем. Ако су умањеник и умањилац дељиви неким бројем, тада је и разлика дељива тим бројем.
Пример: Марко има 21 књигу коју треба да распореди на 7 полица, тако да на свакој буде једнак број књига. Да ли ће он то моћи да уради и кад буде имао три пута више књига?
* Ако је један чинилац производа дељив неким бројем, онда је и производ дељив тим бројем.
То можемо записати и овако: ако c∣a или c∣b тада и c∣аb.
* Ако је неки број дељив неким производом, онда је он дељив сваким од чинилаца тог производа.
То можемо записати и овако: ако ab∣c тада и а∣c тада и b∣c.
* За било која три броја важи: ако a∣b и b∣c тада и a∣c.
Пример: 2∣4 и 4∣16 тада и 2∣16.
* Дељење нулом није изводљиво. Број нула је дељив сваким бројем.
Пример: Који од израза су једнаки нули, а који немају смисла?
а) 0:42, б) (83-(38+45)):2, в) 58:0, г) 49:(64-64), д) 88-(44:0).
Пример: Не израчунавајући производ испитај да ли је:
а) 5|20·123, б) 2|123·29·18, в) 7|49+77-35, г) 2|16·25+31·90.
Пример: Колики може да буде остатак при дељењу неког броја са 2?
Закључак: Сваки природан број можемо записати у једном од облика: 2k (парни бројеви), 2k+1 (непарни бројеви).
Пример: Колики може да буде остатак при дељењу неког броја са 3?
Закључак: Сваки природан број можемо записати у једном од облика: 3k (дељиви са 3), 3k+1 (при дељењу са 3 дају остатак 1), 3k+2 (при дељењу са 3 дају остатак 2).
Пример: Колики може да буде остатак при дељењу неког броја са 4?
Закључак: Сваки природан број можемо записати у једном од облика: 4k (дељиви са 4), 4k+1 (при дељењу са 4 дају остатак 1), 4k+2 (при дељењу са 4 дају остатак 2), 4k+3 (при дељењу са 4 дају остатак 3).
До сада смо научили да ако су оба сабирка дељива неким бројем, тада је и збир дељив тим бројем. Дакле, важи: паран+паран=паран.
Какав је збир парног и непарног броја и збир два непарна броја?
непаран+паран=непаран
непаран+непаран=паран
Како показати да је збир два непарна броја паран. Нека је први непаран број 2k+1, а други 2l+1. Збир ова два броја је 2k+2l+2, a то је паран број.
Долазимо до још једног битног закључка: збир је дељив неким бројем ако је сваки од сабирака дељив тим бројем или ако је збир њихових остатака при дељењу тим бројем дељив тим бројем.
Пример: 7 не дели 15 и 7 не дели 27, и важи 15=7·2+1 и 27=7·3+6, али 7∣15+27, јер 7∣1+6.
* Сваки природан број дељив је јединицом и самим собом.
Пример: Ана има 36 бомбона, а Ивана 48 бомбона. Да ли свака од њих може поделити своје бомбоне у кесице тако да у свакој кесици буду по 4 бомбоне? Ако обједине своје бомбоне да ли их тада могу сместити у кесице по 4 бомбоне?
Дакле, ако 4∣36 и 4∣48, тада и 4∣(36+48). Ово је лако показати, јер ако је 36=4·9 и 48=4·12, тада је 36+48=4·9+4·12=4·(9+12), односно 4∣(36+48). Међутим, ако сабирци нису дељиви неким бројем то не значи да и збир није дељив тим бројем.
Нпр. 2 не дели 17 и 2 не дели 15, али 2 дели 17+15. Исто важи иза разлику.
* Ако су сабирци дељиви неким бројем, онда је и збир дељив тим бројем. Ако су умањеник и умањилац дељиви неким бројем, тада је и разлика дељива тим бројем.
Пример: Марко има 21 књигу коју треба да распореди на 7 полица, тако да на свакој буде једнак број књига. Да ли ће он то моћи да уради и кад буде имао три пута више књига?
* Ако је један чинилац производа дељив неким бројем, онда је и производ дељив тим бројем.
То можемо записати и овако: ако c∣a или c∣b тада и c∣аb.
* Ако је неки број дељив неким производом, онда је он дељив сваким од чинилаца тог производа.
То можемо записати и овако: ако ab∣c тада и а∣c тада и b∣c.
* За било која три броја важи: ако a∣b и b∣c тада и a∣c.
Пример: 2∣4 и 4∣16 тада и 2∣16.
* Дељење нулом није изводљиво. Број нула је дељив сваким бројем.
Пример: Који од израза су једнаки нули, а који немају смисла?
а) 0:42, б) (83-(38+45)):2, в) 58:0, г) 49:(64-64), д) 88-(44:0).
Пример: Не израчунавајући производ испитај да ли је:
а) 5|20·123, б) 2|123·29·18, в) 7|49+77-35, г) 2|16·25+31·90.
Пример: Колики може да буде остатак при дељењу неког броја са 2?
Закључак: Сваки природан број можемо записати у једном од облика: 2k (парни бројеви), 2k+1 (непарни бројеви).
Пример: Колики може да буде остатак при дељењу неког броја са 3?
Закључак: Сваки природан број можемо записати у једном од облика: 3k (дељиви са 3), 3k+1 (при дељењу са 3 дају остатак 1), 3k+2 (при дељењу са 3 дају остатак 2).
Пример: Колики може да буде остатак при дељењу неког броја са 4?
Закључак: Сваки природан број можемо записати у једном од облика: 4k (дељиви са 4), 4k+1 (при дељењу са 4 дају остатак 1), 4k+2 (при дељењу са 4 дају остатак 2), 4k+3 (при дељењу са 4 дају остатак 3).
До сада смо научили да ако су оба сабирка дељива неким бројем, тада је и збир дељив тим бројем. Дакле, важи: паран+паран=паран.
Какав је збир парног и непарног броја и збир два непарна броја?
непаран+паран=непаран
непаран+непаран=паран
Како показати да је збир два непарна броја паран. Нека је први непаран број 2k+1, а други 2l+1. Збир ова два броја је 2k+2l+2, a то је паран број.
Долазимо до још једног битног закључка: збир је дељив неким бројем ако је сваки од сабирака дељив тим бројем или ако је збир њихових остатака при дељењу тим бројем дељив тим бројем.
Пример: 7 не дели 15 и 7 не дели 27, и важи 15=7·2+1 и 27=7·3+6, али 7∣15+27, јер 7∣1+6.
Преузимање
| Deljivost u No, osnovna svojstva.doc | |
| File Size: | 104 kb |
| File Type: | doc |