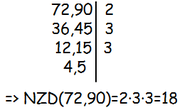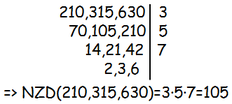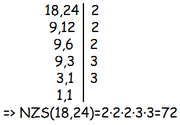Највећи заједнички делилац и најмањи заједнички садржалац
Деф: Делилац датог броја n је сваки природан број којим је тај број дељив, тј. којим се тај број може поделити без остатка. Скуп свих делилаца броја n означава се са Dn.
Нпр., бројеви 1,2,3 6 су делиоци броја 6.
Сваки природан број већи од 1 има бар два делиоца: број 1 и сам тај број. Сваки природан број има коначан број делилаца. Најмањи делилац сваког природног броја је 1, а највећи делилац сваког природног броја је сам тај број.
Пример: Одреди D15, D18, D20, D24.
Заједнички делиоци и највећи заједнички делилац
Пример: Нека је скуп свих делилаца броја 24, а скуп свих делилаца броја 36. Одреди пресек ова два скупа.
Решење: D24={1,2,3,4,6,8,12,24} и D36={1,2,3,4,6,9,12,18,36} , а D24∩D36={1,2,3,4,6,12}.
Означимо D24∩D36=D24,36. Елементи овог скупа су заједнички делиоци бројева 24 и 36. Највећи елемент овог скупа назива се највећи заједнички делилац бројева 24 и 36 и означава се са НЗД24,36).
Деф: Скуп природних бројева којима су дељиви бројеви m и n је скуп заједничких делилаца бројева m и n, у ознаци Dn,m. Највећи од заједничких делилаца природних бројева m и n је њихов највећи заједнички делилац, у ознаци НЗД(m,n).
Другим речима, највећи заједнички делилац два броја је највећи природан број који дели и један и други број.
Нпр., бројеви 1,2,3 6 су делиоци броја 6.
Сваки природан број већи од 1 има бар два делиоца: број 1 и сам тај број. Сваки природан број има коначан број делилаца. Најмањи делилац сваког природног броја је 1, а највећи делилац сваког природног броја је сам тај број.
Пример: Одреди D15, D18, D20, D24.
Заједнички делиоци и највећи заједнички делилац
Пример: Нека је скуп свих делилаца броја 24, а скуп свих делилаца броја 36. Одреди пресек ова два скупа.
Решење: D24={1,2,3,4,6,8,12,24} и D36={1,2,3,4,6,9,12,18,36} , а D24∩D36={1,2,3,4,6,12}.
Означимо D24∩D36=D24,36. Елементи овог скупа су заједнички делиоци бројева 24 и 36. Највећи елемент овог скупа назива се највећи заједнички делилац бројева 24 и 36 и означава се са НЗД24,36).
Деф: Скуп природних бројева којима су дељиви бројеви m и n је скуп заједничких делилаца бројева m и n, у ознаци Dn,m. Највећи од заједничких делилаца природних бројева m и n је њихов највећи заједнички делилац, у ознаци НЗД(m,n).
Другим речима, највећи заједнички делилац два броја је највећи природан број који дели и један и други број.
|
Највећи заједнички делилац два броја најједноставније налазимо на следећи начин: дата два или више броја напишемо један до другог, поред њих повучемо усправну црту и тражимо редом заједничке делиоце тих бројева. Поступак се завршава кад у истом реду буду узајамно прости бројеви. Највећи заједнички делилац једнак је производу простих чинилаца са десне стране црте.
|
Пример: Одреди: a) НЗД(30,45), б) НЗД(72,90), в) НЗД(210,315,630), г) НЗД(168,264,528,336).
Деф: Ако за природне бројеве важи да је НЗД(m,n)=1, тада кажемо да су ти бројеви узајамно прости.
Пример: Одреди НЗД бројева: а) НЗД(11,13), б) НЗД(12,13), в) НЗД(10,49). Који закључак можеш извести?
Два проста броја су и узајамно проста.
Два узастопна природна броја су и узајамно проста.
Два узајамно проста броја не морају бити проста.
Пример: Одреди НЗД бројева: а) НЗД(6,42), б) НЗД(12,144), в) НЗД(10,150). Који закључак можеш извести?
Ако број а дели број b, тада је њихов НЗД(а,b)=a.
Пример: Одреди НЗД бројева: а) НЗД(11,13), б) НЗД(12,13), в) НЗД(10,49). Који закључак можеш извести?
Два проста броја су и узајамно проста.
Два узастопна природна броја су и узајамно проста.
Два узајамно проста броја не морају бити проста.
Пример: Одреди НЗД бројева: а) НЗД(6,42), б) НЗД(12,144), в) НЗД(10,150). Који закључак можеш извести?
Ако број а дели број b, тада је њихов НЗД(а,b)=a.
Садржаоци броја
Деф: Садржалац датог броја n је сваки природан број који је дељив тим бројем. Скуп свих садржалаца броја n означава се са Sn.
Нпр., бројеви 3,6,9,12,15, ... су садржаоци броја 3.
Ако је b делилац броја а, онда је а садржалац броја b. Сваки природан број има бесконачан број садржалаца. Најмањи садржалац сваког природног броја је сам тај број, а највећи садржалац не постоји.
Пример: Одреди S4, S5, S6, S8.
Заједнички садржаоци и најмањи заједнички садржалац
Пример: Пронађи све садржаоце бројева: а) 25, б) 30.
Решење: S25={25,50,75,100,125,150,175,200,...} и S30={30,60,90,120,150,180,210,...}.
Деф: Скуп природних бројева који могу да се поделе без остатка и са m и са n је скуп заједничких садржалаца бројева m и n, у ознаци Sm,n. Најмањи од заједничких садржалаца природних бројева m и n је њихов најмањи заједнички садржалац, у ознаци NZS(m,n), другим речима то је најмањи природан број који може да се подели без остатка и са m и са n.
|
Најмањи заједнички садржалац два броја најједноставније налазимо на следећи начин: дата два или више броја напишемо један до другог, поред њих повучемо усправну црту и тражимо редом делиоце сваког од тих бројева. Поступак се завршава кад у истом реду буду само јединице. Најмањи заједнички садржалац једнак је производу простих чинилаца са десне стране црте. Пример: Одреди: a) NZS(54,90), б) NZS(24,42), в) NZS(15,12,20), г) NZS(18,27,36). |
Пример: Одреди NZS (8,9).
Закључак: Ако су два броја узајамно проста, њихов НЗС је једнак њиховом производу.
Дакле, из NZD (8,9)=1 следи NZS (8,9)=72.
Такође, ако a дели број b, тада је NZD(a,b)=а, a NZS(a,b)=b. На пример, NZD(3,12)=3, a NZS(3,12)=12.
Важи и следеће: m‧n=NZD(n,m)‧NZS(n,m).
Закључак: Ако су два броја узајамно проста, њихов НЗС је једнак њиховом производу.
Дакле, из NZD (8,9)=1 следи NZS (8,9)=72.
Такође, ако a дели број b, тада је NZD(a,b)=а, a NZS(a,b)=b. На пример, NZD(3,12)=3, a NZS(3,12)=12.
Важи и следеће: m‧n=NZD(n,m)‧NZS(n,m).
Преузимање
| NZD i NZS.doc | |
| File Size: | 84 kb |
| File Type: | doc |